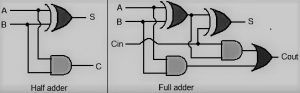
Dodatek Brenta – Kunga został zaproponowany w 1982 roku przez Hsianga Te Kunga i Richarda Peirce'a Brenta. Jest to dodatek do przedrostków równoległych lub dodatek do drzewa, który jest szeroko stosowany w projektowaniu cyfrowym ze względu na jego elastyczność. Równoległe dodatki prefiksów można budować na kilka sposobów w zależności od liczby poziomów logicznych, bramki logiczne zaangażowane, wentylatory z każdej bramy i okablowanie pomiędzy poziomami. Dostępne są różne typy dodatków do drzew, podstawowe dodatki do drzew to Sklanskym KoggeStone i Brent-Kung. W porównaniu do KSA (dodatek Kogge – Stone), ten dodatek zapewnia wysoką regularność struktury sumatora i ma mniejsze blokowanie okablowania co prowadzi do lepszej wydajności i mniejszej wymaganej powierzchni chipa. W tym artykule znajdują się krótkie informacje na temat a Brenta Kunga Addera .
Co to jest Brent Kung Adder?
Sumator wykorzystujący minimalną liczbę obwodów do uzyskania wyniku jest znany jako Brent Kung Adder i jest również znany jako sumator małej mocy lub sumator równoległy. Ten dodatek ma na celu zaoszczędzenie rozmiaru chipa, dzięki czemu produkcja tych dodatków stanie się łatwiejsza. Symetria i zwykła konstrukcja tego dodatku znacznie obniżą koszty produkcji i można go stosować w topologiach rurociągów. Wykorzystanie komplementarnej logiki tranzystora przepustowego pomaga w zwiększeniu wydajności projektu multiplekser podejście w różnych projektach ogniw.
Obwód Addera Brenta Kunga
Poniżej pokazano diagram dodawania przedrostków równoległych brent-kung, który obejmuje etap 1 (etap przetwarzania wstępnego), etapy od 2 do 7 to etapy generowania przeniesienia, a etap 8 to przetwarzanie końcowe. Jest to zaawansowana architektura, bardzo prosta w budowie i zapewniająca mniejsze zatorów w okablowaniu. Zatem mniejsza ilość okablowania zmniejszy ilość miejsca wymaganego do realizacji architektury. Ponadto prowadzenie staje się znacznie łatwiejsze dzięki krzyżowaniu (lub) nakładaniu się mniejszej liczby przewodów. Jednakże kara za opóźnienie wzrośnie z powodu zwiększonej liczby etapów. Zwiększona zostanie wydajność wentylatora dla tego dodatku, a następnie opóźnienie zostanie zwiększone.

Jak działa dodatek Brent Kung?
Brent Kung Adder działa poprzez obliczanie przedrostków dla dwóch grup bitów, co jest przydatne w znajdowaniu przedrostków grup 4-bitowych. Przedrostki te są używane do obliczania przedrostków grupy 8-bitowej itp. Następnie przedrostki te zostaną użyte do obliczenia wykonania określonego etapu bitowego. Przeniesienia te są używane wraz z funkcją Group Propagate następnego etapu w celu obliczenia bitu sumy tego etapu. Brent Kung Tree wykorzystuje 2log2N – 1 stopień.
32-bitowy dodatek Brenta Kunga
Poniżej pokazano 32-bitowy układ dodatku Brenta Kunga. Na początku tego układu projektowane są podstawowe bramki logiczne, takie jak NAND, falownik, XOR, NOR itp. Następnie wraz z bramkami logicznymi projektowane są niezbędne komórki, takie jak czarne i szare komórki, bufory i logika PG.

W poniższym 32-bitowym dodatku Brenta Kunga bramki odwracające, takie jak AOI i OAI, są alternatywnie używane głównie dla szarych i czarnych komórek. Zatem czarne i szare komórki są reprezentowane przez szare i czarne bloki, podczas gdy bufory są reprezentowane przez kółka.


Wejścia takie jak A i B są dostarczane do logiki PG, co pokazano na schemacie blokowym. W przypadku sumatora 32-bitowego potrzebne są 32 bloki logiczne PG, a sygnałami propagacji (P) i generowania (G) są wyjścia tego bloku. Sygnały te dostarczane są do struktury drzewa sumatora Brenta Kunga. Struktura tego dodatku obejmuje szare komórki i czarne komórki.
Szara komórka zawiera trzy wejścia i jedno wyjście. Propagowanie i generowanie sygnałów z bieżącego etapu oraz generowanie sygnałów z poprzedniego etapu to wejścia, natomiast grupa generowania sygnałów to wyjście/wyjście. W dowolnej strukturze drzewa każdy etap zakończy się szarą komórką, a wyjściem tej komórki jest sygnał generowany przez grupę. Sygnał ten jest uważany po prostu za przeniesienie tego etapu. Czarna komórka zawiera cztery wejścia i dwa wyjścia. Wejściami dla tej komórki są sygnały P i G z bieżącego etapu oraz sygnały P, G z poprzedniego etapu.
Logika PG obejmuje bramki AND i XOR, przy czym bramka logiczna AND służy do generowania sygnału G, a bramka logiczna XOR dostarcza sygnał P. Aby wyeliminować niepotrzebne falowniki, stosuje się dwa rodzaje szarych i czarnych komórek. Bramki odwracające używane w jednym rzędzie dla szarej komórki to AOI lub falownik ORAZ, a bramki odwracające dla czarnej komórki w następnym rzędzie wykorzystują falownik OAI lub OR-AND. Komórka AOI wykorzystuje normalne wejścia, aby zapewnić odwrócone wyjścia, podczas gdy OAI wykorzystuje odwrócone wejścia, aby zapewnić normalne wyjścia.
Operacja Brenta Kunga Addera
Dodatek Brenta Kunga to równoległy dodatek przedrostkowy używany do operacji dodawania o wysokiej wydajności. Ten dodatek wygląda jak struktura drzewa, która wykonuje operację arytmetyczną. Ten dodatek obejmuje czarne komórki i szare komórki. Każda czarna komórka ma dwie bramki AND i jedną bramkę OR, a każda szara komórka ma tylko jedną bramkę AND.
Dodatek Brent-kung obejmuje dwa etapy; etap wstępnego przetwarzania i etap wytwarzania. W pierwszym etapie generowanie i propagowanie będzie odbywać się z każdej pary wejść. W tym przypadku propagacja zapewnia operację „XOR” dla bitów wejściowych, podczas gdy generuje operację „AND” dla bitów wejściowych. Propagowanie i generowanie podobnych „Pi” i „Gi” podano poniżej.
Pi = Ai XOR Bi i Gi = Ai ORAZ Bi.
W drugim etapie przeniesienie będzie generowane dla każdego bitu, co jest znane jako generowanie przenoszenia „Cg”, a przeniesienie jest propagowane dla każdego bitu, co jest znane jako generowanie przenoszenia „Cp”. Na potrzeby dalszej operacji zostanie wygenerowane polecenie przenoszenia propagacji i generowania przenoszenia. Ostatnia komórka dostępna w ramach operacji każdego bitu zapewnia przeniesienie. Zatem przenoszenie ostatniego bitu pomoże w sumowaniu następnego bitu jednocześnie aż do ostatniego bitu. Generowanie i propagacja przenoszenia są podane jako;
Cp = P1 ORAZ P0 i Cg=G1 LUB (P1 ORAZ G0)
Stosowany jest głównie do operacji dodawania dwóch trzydziestu dwóch bitów i każdy bit przechodzi etap wstępnego przetwarzania i etap generowania, a następnie zapewnia ostateczną sumę.
Podstawowe bity wejściowe schodzą poniżej etapu przetwarzania wstępnego i powodują propagację i generowanie. Zatem te rozprzestrzeniają się, a także generują, przechodzą etap generowania, generują przenoszenie, generują i przenoszą propagują i zapewniają końcową sumę. Poniżej pokazano krok po kroku proces dodawania Brent-kung.

Układ sumatora Brent-kung wygląda jak struktura drzewiasta i jest to szybki sumator, którego celem jest logika na poziomie bramki. Dodatek ten można zaprojektować ze zmniejszeniem liczby bramek logicznych. W ten sposób zmniejsza opóźnienie i pamięć wykorzystywaną w tej architekturze.
Kod Verilog dodatku Brent Kung Adder
Kod Verilog dodatku Brent Kung pokazano poniżej.
`define INPUTSIZE 64 //ustaw rozmiar wejściowy n
`zdefiniuj GROUPSIZE 8 //ustaw rozmiar grupy = 1, 2, 4 lub 8
moduł Brent_Kung_Adder(A, B, S);
wejście [`INPUTSIZE – 1:0] A;
wejście [`INPUTSIZE – 1:0] B;
wyjście [`INPUTSIZE:0] S;
wire [`INPUTSIZE / `GROUPSIZE * 2 – 1:0] r_temp;
drut [`INPUTSIZE / `GROUPSIZE * 2 – 1:0] r;
drut [`INPUTSIZE / `GROUPSIZE:0] cin;
przewód [`INPUTSIZE / `GROUPSIZE * 2 – 1:0] q;
przypisz cin[0] = 1’b0;
Generować
w której;
for (i = 0; i < `INPUTSIZE / `GROUPSIZE; i = i + 1) rozpocznij: równoległy_FA_CLA_prefiks
group_q_generacja #(.Groupsize(`GROUPSIZE))
F(
.a(A[`ROZMIAR GRUPY * (i + 1) – 1:`ROZMIAR GRUPY * i]),
.b(B[`ROZMIAR GRUPY * (i + 1) – 1:`ROZMIAR GRUPY * i]),
.cin(cin[i]),
.s(S[`ROZMIAR GRUPY * (i + 1) – 1:`ROZMIAR GRUPY * i]),
.qg(q[i * 2 + 1:i * 2])
);
koniec
równoległy_prefix_tree_first_half #(.Treesize(`INPUTSIZE / `GROUPSIZE))
t1(
.q(q[`ROZMIAR WEJŚCIA / `ROZMIAR GRUPY * 2 – 1:0]),
.r(r_temp[`ROZMIAR WEJŚCIA / `ROZMIAR GRUPY * 2 – 1:0])
);
równoległy_prefix_tree_sekunda_half #(.Treesize(`INPUTSIZE / `GROUPSIZE))
t2(
.q(r_temp[`ROZMIARWEJŚCIA / `ROZMIAR GRUPY * 2 – 1:0]),
.r(r[`ROZMIAR WEJŚCIA / `ROZMIAR GRUPY * 2 – 1:0])
);
for (i = 0; i < `INPUTSIZE / `GROUPSIZE; i = i + 1) rozpocząć: cin_generacja
cin_generacja_logika f(
.r(r[2 * i + 1:2 * i]),
.c0(1’b0),
.cin(cin[i + 1])
);
koniec
przypisz S[`INPUTSIZE] = cin[`INPUTSIZE / `GROUPSIZE];
wygenerować końcowo
moduł końcowy
// Pierwsza połowa równoległego drzewa prefiksów
moduł równoległy_prefix_tree_first_half #(parametr Treesize = `INPUTSIZE / `GROUPSIZE)(q, r);
wejście [Rozmiar drzewa * 2 – 1:0] q;
wyjście [Rozmiar drzewa * 2 – 1:0] r;
Generować
w której;
if (Rozmiar drzewa == 2) rozpocznij: trivial_case
przypisz r[1:0] = q[1:0];
prefix_logic f(
.ql(q[1:0]),
.qh(q[3:2]),
.r(r[3:2])
);
zakończ, inaczej zacznij: recursive_case
wire [Rozmiar drzewa * 2 – 1:0] r_temp;
równoległy_prefix_tree_first_half #(.Treesize(Rozmiar drzewa / 2))
rekursja_lsbh(
.q(q[Rozmiar drzewa – 1:0]),
.r(r_temp[Rozmiar drzewa – 1:0])
);
równoległy_prefix_tree_first_half #(.Treesize(Rozmiar drzewa / 2))
rekursja_msbh(
.q(q[Rozmiar drzewa * 2 – 1:Rozmiar drzewa]),
.r(r_temp[Rozmiar drzewa * 2 – 1:Rozmiar drzewa])
);
for (i = 0; i
if (i != Rozmiar drzewa * 2 – 2) rozpocznij: równoległy_ścieg_up_pass
przypisz r[i + 1:i] = r_temp[i + 1:i];
koniec, inaczej zacznij: równoległy_ścieg_up_produce
prefix_logic f(
.ql(r_temp[Rozmiar drzewa – 1:Rozmiar drzewa – 2]),
.qh(r_temp[Rozmiar drzewa * 2 – 1:Rozmiar drzewa * 2 – 2]),
.r(r[Rozmiar drzewa * 2 – 1:Rozmiar drzewa * 2 – 2])
);
koniec
koniec
koniec
wygenerować końcowo
moduł końcowy
// Druga połowa równoległego drzewa prefiksów
moduł równoległy_prefix_tree_sekunda_half #(parametr Treesize = `INPUTSIZE / `GROUPSIZE)(q, r);
wejście [Rozmiar drzewa * 2 – 1:0] q;
wyjście [Rozmiar drzewa * 2 – 1:0] r;
wire [Rozmiar drzewa * 2 * ($clog2(Rozmiar drzewa) – 1) – 1:0] r_temp;
przypisz r_temp[Rozmiar drzewa * 2 – 1:0] = q[Rozmiar drzewa * 2 – 1:0];
Generować
genwar i, j;
for (i = 0; i < $clog2(Rozmiar drzewa) – 2; i = i + 1) rozpocznij: drugi poziom_połowy
przypisz r_temp[Rozmiar drzewa * 2 * (i + 1) + ((Rozmiar drzewa / (2 ** i)) – 1 – 2 ** ($clog2(Rozmiar drzewa / 4) – i)) * 2 – 1:Rozmiar drzewa * 2 * (i + 1)] = r_temp[Rozmiar drzewa * 2 * i + ((Rozmiar drzewa / (2 ** i)) – 1 – 2 ** ($clog2(Rozmiar drzewa / 4) – i)) * 2 – 1: Rozmiar drzewa * 2 * i];
for (j = (Rozmiar drzewa / (2 ** i)) – 1 – 2 ** ($clog2(Rozmiar drzewa / 4) – i); j
prefix_logic f(
.ql(r_temp[Rozmiar drzewa * 2 * i + (j – 2 ** ($clog2(Rozmiar drzewa / 4) – i)) * 2 + 1:Rozmiar drzewa * 2 * i + (j – 2 ** ($clog2( Rozmiar drzewa / 4) – i)) * 2]),
.qh(r_temp[Rozmiar drzewa * 2 * i + j * 2 + 1:Rozmiar drzewa * 2 * i + j * 2]),
.r(r_temp[Rozmiar drzewa * 2 * (i + 1) + j * 2 + 1:Rozmiar drzewa * 2 * (i + 1) + j * 2])
);
if (j != Rozmiar drzewa – 1 – 2 ** ($clog2(Rozmiar drzewa / 4) – i)) rozpocząć: second_half_level_direct_connect
przypisz r_temp[Rozmiar drzewa * 2 * (i + 1) + (j + 2 ** ($clog2(Rozmiar drzewa / 2) – i)) * 2 – 1:Rozmiar drzewa * 2 * (i + 1) + j * 2 + 2] = r_temp[Rozmiar drzewa * 2 * i + (j + 2 ** ($clog2(Rozmiar drzewa / 2) – i)) * 2 – 1:Rozmiar drzewa * 2 * i + j * 2 + 2];
koniec
koniec
przypisz r_temp[Rozmiar drzewa * 2 * (i + 2) – 1:Rozmiar drzewa * 2 * (i + 2) – (2 ** ($clog2(Rozmiar drzewa / 4) – i)) * 2] = r_temp[Rozmiar drzewa * 2 * (i + 1) – 1:Rozmiar drzewa * 2 * (i + 1) – (2 ** ($clog2(Rozmiar drzewa / 4) – i)) * 2];
koniec
przypisz r[1:0] = r_temp[Rozmiar drzewa * 2 * ($clog2(rozmiar drzewa) – 2) + 1:Rozmiar drzewa * 2 * ($clog2(rozmiar drzewa) – 2)];
for (i = 1; i
przypisz r[i * 2 + 1:i * 2] = r_temp[Rozmiar drzewa * 2 * ($clog2(rozmiar drzewa) – 2) + i * 2 + 1:Rozmiar drzewa * 2 * ($clog2(rozmiar drzewa) – 2) + ja * 2];
koniec
for (i = 2; i
prefix_logic f(
.ql(r_temp[Rozmiar drzewa * 2 * ($clog2(Rozmiar drzewa) – 2) + i * 2 – 1:Rozmiar drzewa * 2 * ($clog2(Rozmiar drzewa) – 2) + i * 2 – 2]),
.qh(r_temp[Rozmiar drzewa * 2 * ($clog2(Rozmiar drzewa) – 2) + i * 2 + 1:Rozmiar drzewa * 2 * ($clog2(Rozmiar drzewa) – 2) + i * 2]),
.r(r[i * 2 + 1:i * 2])
);
koniec
wygenerować końcowo
moduł końcowy
moduł group_q_generacja #(parametr Groupsize = `GROUPSIZE)(a, b, cin, s, qg);
wejście [Rozmiar grupy – 1:0] a;
wejście [Rozmiar grupy – 1:0] b;
wejście cin;
wyjście [Rozmiar grupy – 1:0] s;
wyjście [1:0] qg;
drut [2 * Rozmiar grupy – 1:0] q;
przewód [Rozmiar grupy – 1:0] c;
przypisz c[0] = cin;
Generować
w której;
for (i = 0; i < Rozmiar grupy; i = i + 1) rozpocznij: równoległy_FA_CLA_prefiks
FA_CLA_przedrostek f(
.a(a[i]),
.b(b[i]),
.cin(c[i]),
.s(s[i]),
.q(q[i * 2 + 1:i * 2])
);
if (i != Rozmiar grupy – 1) rozpocząć: special_case
przypisz c[i + 1] = q[i * 2 + 1] | (q[i * 2] i c[i]);
koniec
koniec
//grupowanie q w oparciu o wielkość grupy
if (Rozmiar grupy == 1) rozpocznij: case_gs1
przypisz qg[1] = q[1];
przypisz qg[0] = q[0];
zakończ inaczej, jeśli (Grupa == 2) rozpocznij: case_gs2
przypisz qg[1] = q[3] | (q[1] i q[2]);
przypisz qg[0] = q[2] & q[0];
zakończ inaczej, jeśli (Grupa == 4) rozpocznij: case_gs4
przypisz qg[1] = q[7] | (q[5] i q[6]) | (q[3] i q[6] i q[4]) | (q[1] i q[6] i q[4] i q[2]);
przypisz qg[0] = q[6] & q[4] & q[2] & q[0];
zakończ inaczej, jeśli (Grupa == 8) rozpocznij: case_gs8
przypisz qg[1] = q[15] | (q[13] i q[14]) | (q[11] i q[14] i q[12]) | (q[9] i q[14] i q[12] i q[10]) | (q[7] i q[14] i q[12] i q[10] i q[8]) | (q[5] i q[14] i q[12] i q[10] i q[8] i q[6]) | (q[3] i q[14] i q[12] i q[10] i q[8] i q[6] i q[4]) | (q[1] i q[14] i q[12] i q[10] i q[8] i q[6] i q[4] i q[2]);
przypisz qg[0] = q[14] & q[12] & q[10] & q[8] & q[6] & q[4] & q[2] & q[0];
koniec
wygenerować końcowo
moduł końcowy
// Logika generacji Cin
moduł cin_generacja_logic(r, c0, cin);
wejście [1:0] o;
wejście c0;
wyjście cin;
przypisz cin = (r[0] i c0) | r[1];
moduł końcowy
// Podstawowa logika operacji przedrostkowych
moduł prefix_logic(ql, qh, r);
wejście [1:0] ql;
wejście [1:0] qh;
wyjście [1:0] r;
przypisz r[0] = qh[0] & ql[0];
przypisz r[1] = (qh[0] i ql[1]) | qh[1];
moduł końcowy
// Pełna komórka sumująca z przewidywaniem przeniesienia
moduł FA_CLA_prefix(a, b, cin, s, q);
wejście a;
wejście b;
wejście cin;
wyjście s;
wyjście [1:0] q;
przypisz q[0] = a ^ b;
przypisz s = q[0] ^ cin;
przypisz q[1] = a & b;
moduł końcowy
Zalety
Zalety Brent Kung Adder są następujące.
- Jest to sumator o małej mocy, ponieważ do uzyskania wyniku wykorzystuje minimalny obwód.
- Jest to bardzo popularny i szeroko stosowany dodatek.
- Ten rodzaj dodatku można wdrożyć przy użyciu mniejszej liczby modułów w porównaniu z dodatkiem Kogge-Stone.
- Projektowanie sumatora Brenta-Kunga jest bardzo proste.
- Ten dodatek ma mniej połączeń z innymi modułami.
- Dodatki te zaproponowano głównie w celu rozwiązania wad dodatków Kogge-Stone.
Niedogodności
The wady Brenta Kung Adde r uwzględnij następujące elementy.
- Te dodatki mają większe opóźnienie i potrzebują 2 log2 n - 2 poziomów logicznych do obliczenia wszystkich bitów przeniesienia.
- Główną wadą tego sumatora jest rozwarstwienie, które może spowodować rozdzielenie i osłabienie propagacji prądu w sumatorze.
Aplikacje Brent Kung Adder
Zastosowania Brent Kung Adder obejmują następujące.
- Dodatek Brenta – Kunga jest używany w sposób potokowy w celu zmniejszenia zużycia energii poprzez zmniejszenie głębi logiki kombinatorycznej i stabilizację usterek.
- Dodatek Brenta-Kunga zapewnia wyjątkową liczbę etapów od i/p do wszystkich o/ps, ale z asymetrycznym ładowaniem stopni pośrednich.
- Tego dodatku można używać w mnożniku, a także w innych elementach ścieżki danych.
Zatem to jest przegląd Brent kung adder , jego działanie, zalety, wady i zastosowania. Jest to bardzo wydajny dodatek, a jego struktura przypomina strukturę drzewiastą używaną głównie do wykonywania wysokowydajnych operacji arytmetycznych. Ten typ sumatora jest bardzo szybki i koncentruje się głównie na logice na poziomie bramki. Ten dodatek został zaprojektowany przy użyciu mniejszej liczby bramek logicznych. W ten sposób zmniejsza pamięć i opóźnienia wykorzystywane w tej architekturze. Oto pytanie do ciebie, Brent kung adder znany również jako?